Homogeneous spaces

Smooth Manifold

An n-dimensional manifold is a second countable Hausdorff topological space M such that

  • M is locally Euclidean: \forall p \in M, there is U_p \in \tau(p) and a diffeomorphism \phi_p:U_p \rightarrow \widetilde{U}_p \subset \mathbb{R}^n. (U,\phi) is a coordinate system.
  • M has a differentiable structure: there is a collection \mathcal{U}:= \{ (U_{\alpha}) \}_{\alpha \in I} of coordinate systems such that:
    a. M = \cup_{\alpha \in I} U_{\alpha} .
    b. \phi_{\alpha}\circ \phi_{\beta}^{-1} is C^{\infty} .
    c. \mathcal{U} is maximal with respect to (b): if (U, \phi) is a c.s. such that \phi_{\alpha}\circ \phi^{-1} and \phi\circ \phi_{\alpha}^{-1} are smooth, then (U,\phi) \in \mathcal{U} .

Lie groups

  • Lie Group = Smooth manifold + Topological Group
  • U(m)= \{ m \times m \,\,\, \textit{complex matrices such that} \,\,\,A^{*}=A^{-1} \} SO(n)=\{ A \in \mathbb{R}^{n\times n}: det A =1 \}
  • SU(m)=\{ A \in U(m): det A =1 \}

Homogeneous manifolds

  • Let G be a Lie group. If K is an abstract closed subgroup of G, with the relative topology K is a Lie subgroup of G (K is a Lie group, \exists \phi \in Hom(K,G) ), (\phi, K) is a sub-manifold of G: G: d\phi_k:T_kK \rightarrow T_{\phi(k)}G is non-singular \forall k \in K, and \phi is 1 - 1 .
  • Let G be a Lie group. If K is closed subgroup of G, let M = G/H = \{ gK : g \in G \} . Let p:G \rightarrow G/K the natural projection: p(g)=gK . Then, M has a unique manifold structure such
    a. p is C^{\infty} .
    b. There exists local sections of G/K in G : if gK\in M , then there exists W \in \tau(gK) and s\in C^{\infty}(W,G) , such that p\circ s= id_M .
    M above satisfying (a) and (b) is called a homogeneous manifold.

Action of a Lie group on a smooth manifold
An action of G on M is a C^{\infty} – map \cdot : G \times M \rightarrow M such that

  • \forall p \in M, \,\,\, \forall h,g \in G, \,\,\, h\cdot (g\cdot p) = hg \cdot p ,
  • \forall p \in M, \,\,\, e_G \cdot p =p.
  • Effective, if \forall p,q \in M , there exists g=g(p,q)\in G such that g \cdot p=q .
  • Transitive, if

Transitive actions of Lie groups on manifolds
Let \cdot : G \times M \rightarrow M be a transitive action and let p \in M.

  • K = G_p:= \{ g \in G: g \cdot p =p \} is a closed subgroup of G , called the isotropy subgroup at p .
  • The mapping \beta: G / G_p \rightarrow M, \,\,\, gG_p \mapsto g\cdot p, is a diffeomorphism.
  • M\cong G / G_p, \,\,\, \forall p \in M .

Examples:

  • G = SO(n). \,\,\, p \in \mathbb{S}^{n-1}.
    SO(n) \times \mathbb{S}^{n-1} \rightarrow \mathbb{S}^{n-1}
    G_p = SO(n)_p= \{ M \in SO(n) : M \cdot p=p \}\cong SO(n-1) .
    SO(n) / SO(n-1) \cong \mathbb{S}^{n-1} .
  • G = U(n). \,\,\, p \in \mathbb{S}^{2n-1}.
    U(n) \times \mathbb{S}^{2n-1} \rightarrow \mathbb{S}^{2n-1}
    G_p = U(n)_p= \{ M \in U(n) : M \cdot p=p \}\cong U(n-1) .
    U(n) / U(n-1) \cong \mathbb{S}^{2n-1} .
  • G = SU(n). \,\,\, p \in \mathbb{S}^{2n-1}.
    SU(n) \times \mathbb{S}^{2n-1} \rightarrow \mathbb{S}^{2n-1}
    G_p = SU(n)_p= \{ M \in SU(n) : M \cdot p=p \}\cong SU(n-1) .
    SU(n) / SU(n-1) \cong \mathbb{S}^{2n-1} \cong \mathbb{C}\mathbb{P}^{n-1}.
  • SU(2) \cong SU(2) / SU(1) \cong \mathbb{S}^{3} .
  • SU(2)/ \mathbb{T}^1 \cong \mathbb{S}^2 .
    \mathbb{T}^1= \{ diag[ e^{2\pi i \theta}, e^{-2\pi \theta}]: \theta \in [0,1] \} .

Hopf fibration:

  • SU(2)/ \mathbb{T}^1 \cong \mathbb{S}^2 .
  • \mathbb{SU}(2) \cong \mathbb{S}^3, \,\,\, \mathbb{T}^1 \cong \mathbb{S}^1 .
  • \mathbb{S}^3/ \mathbb{S}^1 \cong \mathbb{S}^2 .

Fibration I = [0,1] .

A continuous surjection p: E \rightarrow F is a fibration, if \forall X, (X,p) has the Homotopy lifting property:
– \forall f: X \times I \rightarrow B,
– \forall \widetilde{f}_0 : X \times I \rightarrow E lifting f_0 = f|_{X\times\{0\}},
– There exists \widetilde{f}:X \times I \rightarrow E f to E : f=p\circ \widetilde{f} .

Hopf Fibration.

There is a continuous surjection p \mathbb{S}^3 \rightarrow \mathbb{S}^2 such that \forall X, \,\,\, (X,p) has the Homopoty lifting property:

Vector Bundles. 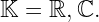\mathbb{K} = \mathbb{R},\mathbb{C}.

A C^{\infty} \,\,\,\,\, \mathbb{K} – vector bundle is a triple (p,E,M), where p : E \rightarrow M is a C^{\infty} surjection such that:
(i) \forall x \in M, \,\,\, E_x = p^{-1}(x) is a \mathbb{K}-vector space.
(ii) \forall x \in M, \exists U \in \tau(x), and a homeomorphism \phi : E_U:= p^{-1}(U) \rightarrow U \times \mathbb{K}^n is a linear mapping; (ii) says that E is trivial in U .
(iii) There exists an open covering \mathfrak{U} = \{ U_i\}_{i\in I} of M: \forall x \in M, there exists U_i, such that x \in U_i \subset M, with E being trivial in U_i.

Examples:
– Trivial vector bundles: E = B\times \mathbb{K}^n, \,\,\, p:E \rightarrow B, \,\,\, p(b,v)=b.
– Tangent bundle: TM \rightarrow M.

Examples:
Line bundle on the real projective plane \mathbb{R}\mathbb{P}^n.
– u,v \in \mathbb{S}^n, \,\,\, u \sim v \Leftrightarrow u=-v. \,\,\, \mathbb{R}\mathbb{P}^n = \mathbb{S}^n/ \sim.
– \gamma_n = \{ (x,l):x \in \mathbb{R}\mathbb{P}^n, l \in \mathbb{R}u\}.
– p: \gamma_n \rightarrow \mathbb{R}\mathbb{P}^n is called the line bundle of \mathbb{R}\mathbb{P}^n.
– \gamma_1 \rightarrow \mathbb{R}\mathbb{P}^1 = \mathbb{S}^1 is the infinite Möbius band.

Some papers about homogeneous manifolds:

  • Kumar V., Ruzhansky M., Hausdorff-Young inequality for Orlicz spaces on compact homogeneous manifolds, Indag. Math., 31 (2020), 266-276. link, arxiv
  • Akylzhanov R., Nursultanov E., Ruzhansky M., Hardy-Littlewood, Hausdorff-Young-Paley inequalities, and Lp-Lq Fourier multipliers on compact homogeneous manifolds, J. Math. Anal. Appl., 479 (2019), 1519-1548. arxiv, link
  • Daher R., Delgado J., Ruzhansky M., Titchmarsh theorems for Fourier transforms of Holder-Lipschitz functions on compact homogeneous manifolds, Monatsh. Math., 189 (2019), 23-49. arxiv, link (open access)
  • Nursultanov E., Ruzhansky M., Tikhonov S., Nikolskii inequality and Besov, Triebel-Lizorkin, Wiener and Beurling spaces on compact homogeneous manifolds, Ann. Sc. Norm. Super. Pisa Cl. Sci., 16 (2016), 981-1017. arxiv, link
  • Dasgupta A., Ruzhansky M., Gevrey functions and ultradistributions on compact Lie groups and homogeneous spaces, Bull. Sci. Math., 138 (2014), 756-782. offprint (open access), arxiv, link