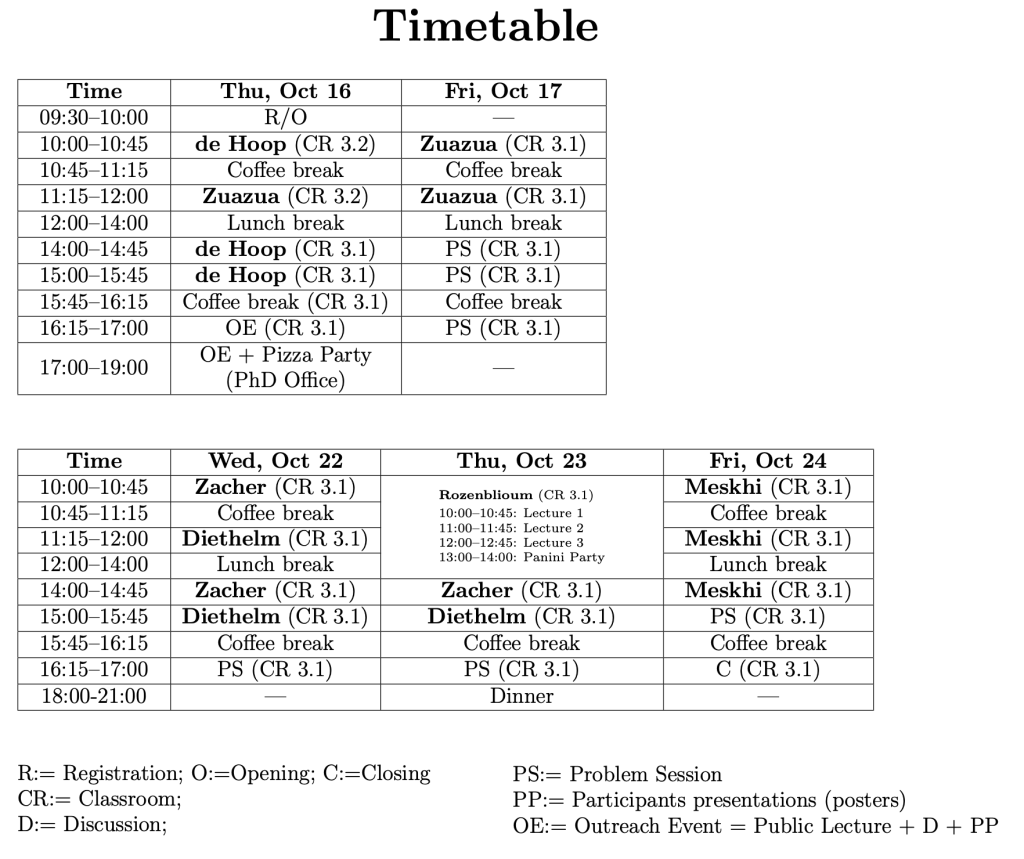
From October 16 to 24, 2025, we organise a school on PDEs entitled “Oscillation phenomena, PDEs, and applications: A Comprehensive School in Mathematical Analysis.”
🎓 Lecturers: The list of speakers includes distinguished experts in the field of partial differential equations:
Maarten de Hoop (Rice University): Spectral analysis of terrestrial planets and gas giants (week 1)
Abstract: We characterize the spectrum of rotating planets. In the first lecture, we consider the case of a simplified gas planet through truncation such that the surface density is non-vanishing. We determine the essential spectrum associated with gravito-inertial (gi) modes, in addition to the discrete spectrum associated with acoustic (p) modes, starting from the acoustic-gravitational system of linear equations for seismology supplemented with appropriate boundary conditions in a rotating reference frame. We do not impose incompressibility as the fluid does support acoustic modes. We depart from assumptions invoking symmetry or homogeneity, when the component of the spectrum associated with gravito-inertial modes is no longer pure point or everywhere dense. For the characterization of the spectra we introduce a modification of the classical Helmholtz decomposition and Leray projector (with range reminiscent of the anelastic approximation) while assuming “general” spatial variability in the parameters such as density of mass and Brunt-Väisälä frequency. The mentioned decomposition gives a zero dynamic pressure component and a corresponding potential component. Using the Schur complement, this decomposition naturally splits the spectrum into one component that can be associated with acoustic modes, and a second component comprising gravito-inertial modes. In the second lecture, we prove that the essential spectrum entirely corresponds with the second component. We first analyze the gravito-inertial modes using techniques from microlocal analysis in the interior, and then develop a reformulation into a large system of PDEs to handle the boundary. We show that, when certain ellipticity conditions are satisfied, this system satisfies the Lopatinskii conditions. We then, briefly, adapt the analysis above to outer cores of terrestrial planets like Earth or Mars. In the third, advanced lecture, we consider gas giants like Saturn or Jupiter. On gas giants the speed of sound goes to zero at the surface. Geometrically, this corresponds to a Riemannian manifold whose metric tensor has a conformal blow-up near the boundary; the blow-up is tamer than in asymptotically hyperbolic geometry, that is, the boundary is at a finite distance. We sketch a proof of the existence of a discrete, acoustic spectrum using the zero-pseudodifferential calculus.
Kai Diethelm (Technische Hochschule Würzburg-Schweinfurt): Fractional Differential Operators (week 2)
Lecture 1. Introduction to Fractional Differential Operators
Lecture 2. Fractional Diffusion Equations, Part 1
Lecture 3. Fractional Diffusion Equations, Part 2
Alexander Meskhi (Kutaisi International University, TSU A. Razmadze Mathematical Institute): Sobolev and trace inequalities, and sharp norm estimates for fractional integrals (week 2)
Abstract: Our aim is to discuss the criteria for trace inequalities for the Riesz potential and Riemann–Liouville operators in classical Lebesgue spaces. We will discuss necessary and sufficient conditions on measures guaranteeing Sobolev-type inequalities and compactness for fractional integral operators defined by non-doubling measures. Furthermore, we will present sharp weighted estimates (sharp Olsen inequalities) for fractional integral operators in Morrey spaces. Both linear and multilinear fractional integrals will be treated.
Grigori Rozenblum (Chalmers University of Technology, The University of Gothenburg): Eigenvalue Estimates for Schrödinger Operators, Using Sobolev Embedding Theorems (week 2)
Abstract: Let V(x), x \in \mathbb{R}^d, be a function (“electric potential”). The Schrödinger operator, H(V) = -\Delta – V(x) is one of the most important objects in quantum physics, and its spectrum describes the properties of the quantum system. Let N^{-}(V) denote the number of negative eigenvalues of H(V). The CLR estimate, proved by the lecturer in 1972, states N^{-}(V) \leq C(d)\int (V(x)^{+})^{d/2}dx, for d \geq 3, valid for all V for which the integral converges. This estimate and its generalizations have had numerous applications in mathematics, quantum and classical physics. Various proofs have been proposed, using quite different ideas. In the minicourse, the original (and most elementary) proof will be explained, which is based upon Sobolev embedding theorems. Quite recently, it was found that this method can be adapted to establishing eigenvalue estimates for Schrödinger operators where the role of potential V is played by a measure, singular with respect to the Lebesgue measure. This produces eigenvalue estimates for several important physical models. These extensions will also be explained.
Expected knowledge: Basics of Hilbert space, Self-adjoint operators, Sobolev embedding theorem, Basics of measure theory
Recommended introductory literature: Schrödinger Operators: Eigenvalues and Lieb–Thirring Inequalities by R. Frank, A. Laptev, T. Weidl, Cambridge 2022; G. Rozenblum, E. Shargorodsky, 2021: MR4331823; G. Rozenblum, G. Tashchiyan, 2022: MR4484835; G. Rozenblum, 2025, Doc.Math., ArXiv:2405.03335
Rico Zacher (University of Ulm): Li-Yau and Harnack estimates for nonlocal diffusion problems (week 2)
Abstract: I will present recent results on differential Harnack inequalities of Li-Yau type for a large class of nonlocal diffusion equations. This includes problems on infinite discrete structures (graphs) on which arbitrarily long jumps are possible, problems in Euclidean space with a fractional Laplace operator and hybrid problems in a discrete-continuous setting which cover certain systems of reaction-diffusion equations. One of the main difficulties is that the classical chain rule is not valid for the nonlocal operators under consideration. Additionally, if one wants to adopt Li and Yau’s approach from their
famous 1986 paper (Acta. Math.), new curvature-dimension (CD) inequalities are required, since the classical Bakry-Emery condition based on the Gamma calculus is no longer suitable. This also touches on the fundamental question of how to define lower curvature bounds on discrete structures in a meaningful way. In addition to the approach using CD inequalities, I will present another method which is based on heat kernel representations of the solutions and consists in reducing the problem to the heat kernel. I will also show that the new nonlocal Li-Yau type estimates are strong enough to derive
Harnack inequalities.
Enrique Zuazua (Friedrich Alexander University of Erlangen-Nürnberg): PDE controllability and Machine Learning (week 1)
Lecture 1. PDE controllability Controllability theory for Partial Differential Equations (PDEs) lies at the crossroads of analysis, geometry, and applications. It addresses a fundamental question: to what extent can we steer the evolution of a distributed system, governed by a PDE, toward a desired state by acting through suitable inputs or controls? Over the past decades, controllability has matured into a vibrant field, with key results for parabolic, hyperbolic, and dispersive equations, and with deep connections to optimization, numerical analysis, and, more recently, machine learning. In this lecture, I will present the main ideas and techniques underlying PDE controllability: observability inequalities, unique continuation principles, microlocal analysis, and Carleman estimates. I will also highlight several emblematic results, from exact controllability of the wave equation to null controllability of the heat equation, and discuss the interplay between control cost, geometry, and system dynamics.
Lecture 2. Waves: Propagation, control, and numerical approximations Wave-like equations arise in many areas of science and engineering, where controlling their behavior is often crucial for applications ranging from structural vibrations to acoustics and electromagnetics. A central difficulty in the controllability of such systems is the presence of high-frequency components, which can obstruct observability estimates and degrade the effectiveness of control strategies. These challenges are amplified in numerical approximations: standard discretization schemes often generate spurious high-frequency oscillations that are invisible to the control mechanism, leading to severe instabilities and loss of convergence. In this lecture, we will review the mathematical foundations of controllability for wave-like equations and analyze the obstacles posed by high-frequency phenomena. We will then discuss numerical methods designed to overcome these difficulties, including filtering techniques, adapted discretizations.
Lecture 3. Control and Machine Learning
Systems control, or cybernetics—a term first coined by Ampère and later popularized by Norbert Wiener—refers to the science of control and communication in animals and machines. The pursuit of this field dates back to antiquity, driven by the desire to create machines that autonomously perform human tasks, thereby enhancing freedom and efficiency. The objectives of control systems closely parallel those of modern Artificial Intelligence (AI), illustrating both the profound unity within Mathematics and its extraordinary capacity to describe natural phenomena and drive technological innovation. In this lecture, we will explore the connections between these mathematical disciplines and their broader implications. We will also discuss our recent work addressing two fundamental questions: Why does Machine Learning perform so effectively? And how can data-driven insights be integrated into the classical applied mathematics framework, particularly in the context of Partial Differential Equations (PDE) and numerical methods? This effort is leading us to a new emerging field of PDE+D(ata) in parallel to the development of new Digital Twins technologies.`
Zoom link to join: https://us02web.zoom.us/j/83095584409?pwd=c3huaUhZcWFrZ2NNMU05Ujg4aUlWQT09
Meeting ID: 830 9558 4409
Passcode: 135803
🕒 Program:

We are pleased to announce the public lecture entitled “Machine Learning: A Mathematician’s Perspective”, to be delivered by Prof. Enrique Zuazua (Friedrich Alexander University Erlangen–Nürnberg) on Thursday, October 16, at 16:15 (Campus Sterre, Building S8).
A poem generated by Generative AI about a PDE team in Ghent who also like pizzas:
“The PDEs of Pizza”
In Ghent’s old streets where scholars dwell,
A team of minds knows PDEs well.
They model waves, they tame the heat,
But never miss a slice to eat.
They speak of Laplace late at night,
Of Navier–Stokes and boundary plight.
While eigenvalues softly hum,
The pizza timer ticks — it’s done!
From finite elements to crusts so thin,
They solve, they slice, they both begin.
A theorem proved, a topping spread,
A steady state of cheese and bread.
Convection, diffusion, or maybe advection,
All find balance in yeast’s perfection.
Their gradients rise, their norms align,
And pizza’s curl is truly fine.
So here’s to Ghent’s bright PDE band,
With floury fingers, chalk in hand.
For though their proofs may never cease —
They always find a slice of peace. 🍕
Group photo week 1

Group photo week 2

📝 Registration (closed):
We ask participants to register via the following registration form:
For those who wish to attend only the public lecture in person, please complete the registration form below so that we can estimate the number of participants:
🎯 Targeted Audience: The school is open to anyone. For more information you can contact us by email at analysis.pde@ugent.be. The school will be free of charge for UGent PhD candidates. Other participants (in person) will be charged €10 per day to cover organisational expenses.
🌐 Public Outreach Event: A public lecture, poster session, and networking reception will complement the school, fostering engagement with a wider audience.
🏛️ Location: Campus Sterre, Krijgslaan 297, 9000 Gent, gebouw S8!
👥 Organising and Scientific Committee: Michael Ruzhansky, Duvan Cardona, Marianna Chatzakou, Hendrik De Bie, Karel Van Bockstal
PhD Organising Committee: Irfan Ali, David Santiago Gomez Cobos, Zhipeng Song
🌟 Seasonal School Workshop I 🌟
As a continuation of the school, we are delighted to host a follow-up workshop on Artificial Intelligence and Signal Processing. The speakers are Prof. Sven Nõmm (Tallinn University of Technology, Estonia) and Prof. Haihui Wang (Beihang University, China).
Date and Time: Wednesday, 12th November 2025, 3:00-6:00 PM CET, Lecture Room 3.1 in S8
Talk 1 (3:00-4:00 PM): Sven Nõmm. Who will Guard the Guardians in the age of AI: From the simple AI concepts to the problems of explainable AI
Abstract: The question of why certain decisions were made by an AI-based algorithm was asked nearly 50 years ago. Today, in many areas where AI is used, it has become mandatory to answer this question. Nevertheless, be careful with what you are asking for! Explaining such decisions is not an easy task. During this talk, we will provide a brief overview of what AI as a discipline is, how it makes decisions, and how the need to explain these decisions has emerged. Then we will review the main explanation techniques, their quality and the emerging gap in applying them.
Talk 2-3 (4:00-6:00 PM): Haihui Wang. Time-frequency analysis: theory and applications
Abstract: This talk first introduces several methods for stationary and non-stationary signal processing, including the Fourier Transform, Short-Time Fourier Transform (STFT), S-Transform, Empirical Mode Decomposition (EMD), and Wavelet Transform. The applications of these methods are then analyzed using both analog and real-world signals. Experimental results demonstrate that the selection of an algorithm should depend on the characteristics of the signals. Finally, several case studies are presented, combining time–frequency feature extraction with machine learning and deep learning techniques.
Date and Time: Friday, 14th November 2025, 2:00-3:00 PM CET, Lecture Room 3.2 in S8
Talk 4 (3:00-4:00 PM): Sven Nõmm. Research in the age of AI
Abstract: The question of why certain decisions were made by an AI-based algorithm was asked nearly 50 years ago. Today, in many areas where AI is used, it has become mandatory to answer this question. Nevertheless, be careful with what you are asking for! Explaining such decisions is not an easy task. During this talk, we will provide a brief overview of what AI as a discipline is, how it makes decisions, and how the need to explain these decisions has emerged. Then we will review the main explanation techniques, their quality and the emerging gap in applying them.
Please note that this talk will be held in hybrid mode, both in person and via Zoom.
Zoom link to join: https://us02web.zoom.us/j/83095584409?pwd=c3huaUhZcWFrZ2NNMU05Ujg4aUlWQT09
Meeting ID: 830 9558 4409
Passcode: 135803
The Doctoral School Office of Ghent University has recognised the school as a specialist course/seasonal school as part of Ghent University’s doctoral training programme. A maximum of 18,000€ is awarded for the organisation of this event. It is the fourth event in a series of schools supported by the UGent Doctoral Schools:
- 2024: Summer School “Direct and Inverse Problems with Applications, and Related Topics: A Comprehensive Summer School in Mathematical Analysis”: https://analysis-pde.org/summer-school-direct-and-inverse-problems-with-applications-and-related-topics/
- 2023: Summer School “Modern Problems in PDEs and Applications”: https://analysis-pde.org/summer-school-modern-problems-in-pdes-and-applications/
- 2022: Summer School “Singularities in Science and Engineering”: https://analysis-pde.org/summer-school-singularities-in-science-and-engineering/



